Étienne Ghys : La musique des formes.

« L’invité », est une nouvelle rubrique qui, comme son nom l’indique, invite une personnalité, extérieure au monde musical contemporain, à s’exprimer sur sa relation à la musique. Notre premier invité est un grand mathématicien, Étienne Ghys, qui est aussi connu pour ses travaux de vulgarisation à destination du grand public.

J’ai eu très peu de rapport intime à la musique dans ma vie. Mon père était sourd et la musique était totalement absente à la maison. Quand j’ai eu neuf ou dix ans, mon instituteur m’a convaincu d’entrer dans une chorale. J’aimais bien — même si c’était une chorale catholique et que je devais chanter trois messes tous les dimanches. Ce même instituteur m’a bientôt donné quelques cours de solfège, après l’école. Trouvant que je me débrouillais bien, il a essayé de convaincre mes parents de me mettre à un instrument. En vain. Dans leur esprit, je pense que la musique était réservée aux élites, dont nous n’étions pas. Ça a marqué la fin de ma « carrière musicale ». J’écoute toutefois beaucoup de musique, surtout de l’opéra, mais sans aucun savoir savant sur le sujet.

Cependant, quand je regarde rétrospectivement ma vie de mathématicien, je m’aperçois que le son y joue un rôle. C’est toujours dans des moments acoustiquement chaotiques que me sont venues les quelques idées fulgurantes que j’ai eues. Je pense par exemple au métro de New York, avec ces rames qui font un bruit insupportable, mais dans lesquelles j’ai enfin compris comment marchaient les complexes difféomorphismes d’Anosov qui me résistaient depuis longtemps. Je ne sais si le phénomène a une explication neurologique, mais le chaos sonore me fait le plus grand bien. Ayant raconté cette anecdote à une connaissance, celle-ci m’a offert un disque de Thomas Adès. Je l’écoute souvent. L’une des œuvres, Living Toys, me rappelle le vacarme chaotique du métro de New York.

S’il est un aspect qui rapproche les mathématiques de la musique — et, plus largement, de la création artistique —, c’est sa beauté, son esthétique, qui n’est peut-être, hélas, accessible qu’aux initiés, mais qui, je pense, est le principal moteur des chercheurs comme moi. Si on considère tout le spectre des scientifiques, du mathématicien au médecin, je pense que les mathématiciens sont les plus proches des artistes. Les applications concrètes les motivent rarement. Celles-ci sont évidemment très utiles dans le domaine des mathématiques appliquées, mais la plupart des mathématiciens sont d’abord et principalement intéressés par la beauté intrinsèque que recèlent les maths. Cette recherche de beauté, cette forme de gratuité, caractérisent aussi l’artiste.

Un autre lien, historique celui-ci, entre mathématique et musique, est bien évidemment la théorie pythagoricienne des cordes vibrantes qui fonde l’harmonie. À cet égard, en tant que science des rapports numériques, la musique fait partie depuis l’Antiquité et jusqu’à la Renaissance des sept arts libéraux de l’enseignement, et plus particulièrement du quadrivium qui se rapporte au pouvoir des nombres — aux côtés de l’arithmétique, de la géométrie et de l’astronomie.

La théorie des cordes vibrantes m’amène à un sujet qui entre davantage dans mon champ de compétence : il existe ainsi un thème purement mathématique qui a pour origine, certes lointaine, une question d’acoustique et de musique. Pour cela revenons un instant sur cette corde vibrante : lorsqu’une corde (de violon ou de guitare) vibre, son mouvement peut se décomposer en une série de fréquences successives qui sont toutes multiples d’une fréquence fondamentale. L’addition de toutes ces fréquences (et de leur amplitude dans le spectre) donne le timbre de la corde, de l’instrument. C’est comme ça que notre oreille reconnaît que c’est une corde qui vibre. Chaque instrument vient ainsi avec son timbre, qui correspond à la série des fréquences qui composent son spectre.

Prenons à présent un tambour et tapons dessus. Sans même regarder, à l’oreille, tout le monde sait distinguer le son d’un tambour de celui d’un violon. Mais comment ? L’explication, c’est que les vibrations du tambour sont elles aussi superpositions de vibrations élémentaires mais, contrairement à la corde de violon, les fréquences des harmoniques ne sont pas espacées régulièrement.

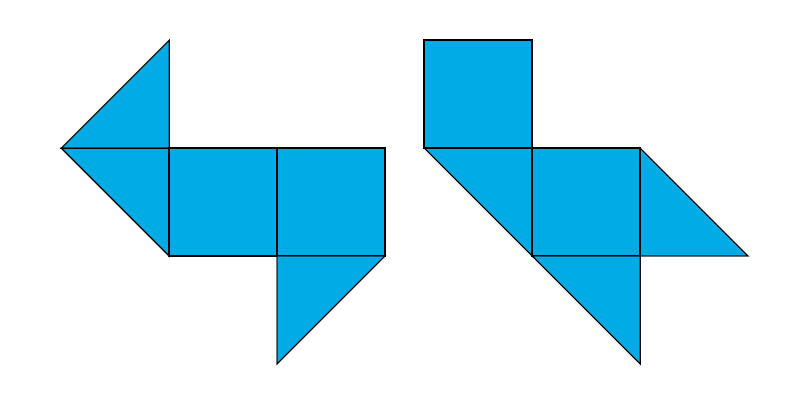
En 1966, un mathématicien appelé Mark Kac a ainsi posé la question : Peut-on entendre la forme d’un tambour ? Par forme du tambour, il veut parler de la forme de la membrane (et non celle de sa caisse de résonance). Traduit en termes mathématiques, cela revient à se demander si la signature fréquentielle d’un tambour dépend de la forme de sa membrane. Lorsqu’on songe à un tambour, on l’imagine tacitement circulaire. Mais que se passe-t-il s’il est carré ou ovale ?

Depuis ce premier article, de nombreux mathématiciens, et non des moindres, ont planché sur le sujet et ont établi quelques résultats préliminaires : par exemple, on a démontré assez rapidement que le spectre peut déterminer si un tambour est circulaire — et ce, quelle que soit la taille du cercle. On a aussi démontré que le spectre permet de déterminer la superficie de la membrane (en cm2) ainsi que son périmètre. Mais pas encore sa forme. C’est ainsi qu’on a progressé, pas à pas. Jusqu’à ce que, en 1992, on trouve un vrai contre-exemple : c’est-à-dire deux formes de membrane différentes qui produisent le même timbre (illustration ci-dessous). Sauf qu’aucun musicien, jamais, n’aurait l’idée de tambours de cette forme-là !

Propos recueillis par Jérémie Szpirglas

Photo : DR